Energía cinética
En física, la energía cinética de un cuerpo es aquella energía que posee debido a su movimiento. Se define como el trabajonecesario para acelerar un cuerpo de una masa determinada desde el reposo hasta la velocidad indicada. Una vez conseguida esta energía durante la aceleración, el cuerpo mantiene su energía cinética salvo que cambie su velocidad. Para que el cuerpo regrese a su estado de reposo se requiere un trabajo negativo de la misma magnitud que su energía cinética. Suele abreviarse con letra Ec oEk (a veces también T o K)
.
.
Energía cinética en diferentes sistemas de referencia[editar]
Como hemos dicho, en la mecánica clásica, la energía cinética de una masa puntual depende de su masa  y sus componentes del movimiento. Se expresa en julios (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad
y sus componentes del movimiento. Se expresa en julios (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad  de la masa puntual, así:
de la masa puntual, así: 
 y sus componentes del movimiento. Se expresa en julios (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad
y sus componentes del movimiento. Se expresa en julios (J). 1 J = 1 kg·m2/s2. Estos son descritos por la velocidad  de la masa puntual, así:
de la masa puntual, así: 
En un sistema de coordenadas especial, esta expresión tiene las siguientes formas:
- Coordenadas cartesianas (x, y, z):
Con eso el significado de un punto en una coordenada y su cambio temporal se describe como la derivada temporal de su desplazamiento:
En un formalismo hamiltoniano no se trabaja con esas componentes del movimiento, o sea con su velocidad, sino con su impulso  (cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:
(cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:
 (cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:
(cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:Energía cinética de sistemas de partículas[editar]
Para una partícula, o para un sólido rígido que no este rotando, la energía cinética cae a cero cuando el cuerpo para. Sin embargo, para sistemas que contienen muchos cuerpos con movimientos independientes, que ejercen fuerzas entre ellos y que pueden (o no) estar rotando, esto no es del todo cierto. Esta energía es llamada 'energía interna'. La energía cinética de un sistema en cualquier instante de tiempo es la suma simple de las energías cinéticas de las masas, incluyendo la energía cinética de la rotación.
Un ejemplo de esto puede ser el Sistema Solar. En el centro de masas del sistema solar, el Sol está (casi) estacionario, pero los planetas y planetoides están en movimiento sobre él. Así en un centro de masas estacionario, la energía cinética está aún presente. Sin embargo, recalcular la energía de diferentes marcos puede ser tedioso, pero hay un truco. La energía cinética de un sistema de diferentes marcos inerciales puede calcularse como la simple suma de la energía en un marco con centro de masas y añadir en la energía el total de las masas de los cuerpos que se mueven con velocidad relativa entre los dos marcos.
Esto se puede demostrar fácilmente: sea V la velocidad relativa en un sistema k de un centro de masas i:
Donde:
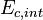 , es la energía cinética interna respecto al centro de masas de ese sistema
, es la energía cinética interna respecto al centro de masas de ese sistema es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas.
es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas. , es la masa total.
, es la masa total.
Por lo que la expresión anterior puede escribirse simplemente como:1
Donde puede verse más claramente que energía cinética total de un sistema puede descomponerse en su energía cinética de traslación y la energía de rotación alrededor del centro de masas. La energía cinética de un sistema entonces depende del Sistema de referencia inercial y es más bajo con respecto al centro de masas referencial, por ejemplo, en un sistema de referencia en que el centro de masas sea estacionario. En cualquier otro sistema de referencia hay una energía cinética adicional correspondiente a la masa total que se mueve a la velocidad del centro de masas.
Energía cinética de un sólido rígido en rotación
Para un sólido rígido que está rotando puede descomponerse la energía cinética total como dos sumas: la energía cinética de traslación (que es la asociada al desplazamiento del centro de masa del cuerpo a través del espacio) y la energía cinética de rotación (que es la asociada al movimiento de rotación con cierta velocidad angular). La expresión matemática para la energía cinética es:
Donde:
 Energía de traslación.
Energía de traslación.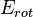 Energía de rotación.
Energía de rotación. Masa del cuerpo.
Masa del cuerpo. tensor de (momentos de) inercia.
tensor de (momentos de) inercia. velocidad angular del cuerpo.
velocidad angular del cuerpo. traspuesta del vector de la velocidad angular del cuerpo.
traspuesta del vector de la velocidad angular del cuerpo. velocidad lineal del cuerpo.
velocidad lineal del cuerpo.
El valor de la energía cinética es positivo, y depende del sistema de referencia que se considere al determinar el valor (módulo) de la velocidad  y
y  . La expresión anterior puede deducirse de la expresión general:
. La expresión anterior puede deducirse de la expresión general:
 y
y  . La expresión anterior puede deducirse de la expresión general:
. La expresión anterior puede deducirse de la expresión general:Energía Cinética
La energía cinética (siglas en inglés K.E.) es la energía del movimiento. La energía cinética de un objeto es la energía que posee a consecuencia de su movimiento. La energía cinética* de un punto material m está dada por

La energía cinética es una expresión del hecho de que un objeto en movimiento, puede realizar un trabajo sobre cualquier cosa que golpee; cuantifica la cantidad de trabajo que el objeto podría realizar como resultado de su movimiento. La energía mecánica total de un objeto es la suma de su energía cinética y su energía potencial.
Para un objeto de tamaño finito, esta energía cinética se llama la energía cinética de traslación de la masa, para distinguirlo de cualquier energía cinética rotacional que puede poseer. La energía cinética total de una masa, se puede expresar como la suma de la energía cinética de traslación de su centro de masa, más la energía cinética de rotación alrededor de su centro de masa.
*Se supone que la velocidad es mucho menor que la velocidad de la luz. Si la velocidad es comparable a c, se debe usar la expresión de la energía cinética relativista.

 ):
):
 ):
):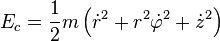
 ):
):![E_c=\frac{1}{2}m \left(r^2 \left[\dot \theta^2 + \dot \varphi^2 \sin^2\theta \right] + \dot r^2 \right)](http://upload.wikimedia.org/math/1/b/6/1b63189e3cca32b06f6f4ede5a1bf61b.png)


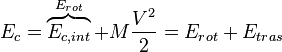
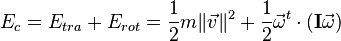
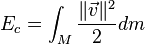
No hay comentarios:
Publicar un comentario